现代控制理论

第一章

现代控制理论和经典控制理论的区别

• 经典控制理论主要研究单输入单输出线性时不变系统，现代控制理论可以解决多输入多输出系统、非线性系统和时变系统等控制问题。

• 相比经典控制理论, 现代控制理论考虑问题更全面、更复杂, 主要表现在考虑系统内部之间的耦合,系统外部的干扰, 但符合从简单到复杂的规律。

第二章

系统状态空间表达式要会写

状态空间表达式的状态变量图

同一系统的各种模型间可以互相转化：重点，必考

• 常微分方程模型中不含输入函数的导数
• 状态空间模型化为传递函数模型：$G(s)=C(sI-A)^{-1}B+D$
• 传递函数不变性证明：PPT第45页
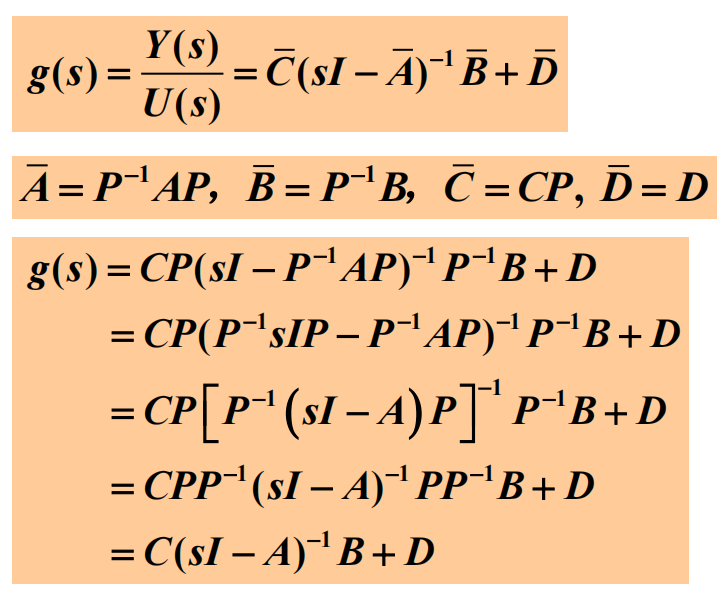
• 由传递函数建立状态空间表达式（求状态空间实现）——直接分解法、串联分解和并联分解。

  • 直接分解法：

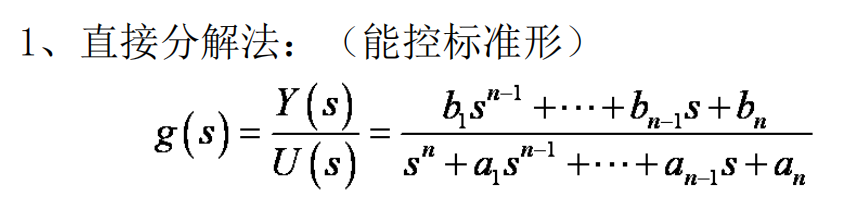
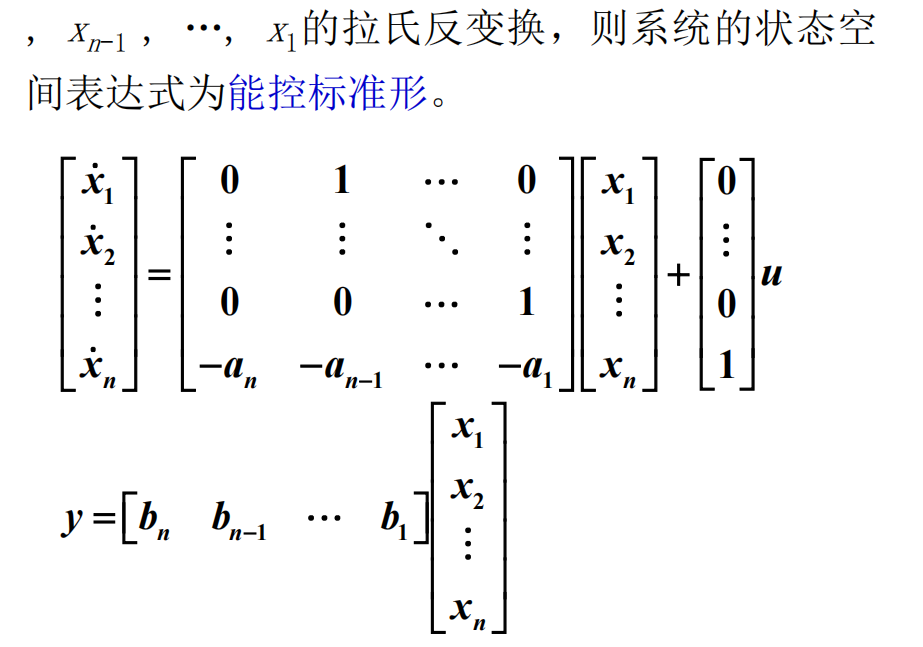
  • 串联分解法：

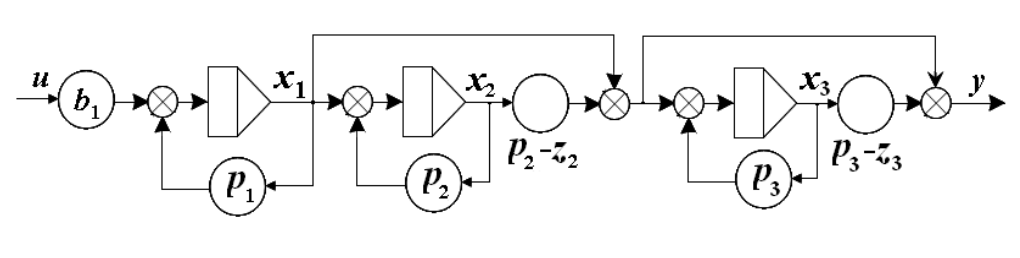
  • 并联分解法：

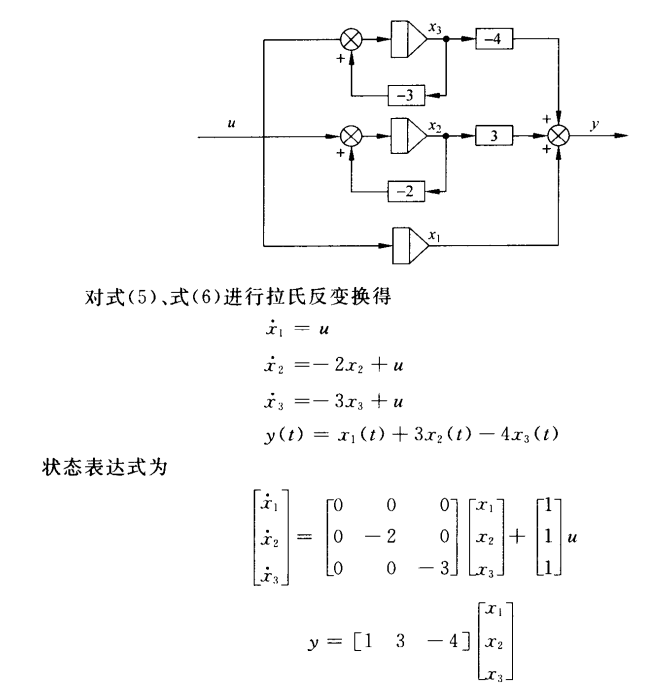
• 差分方程化为状态空间表达式：差分方程中不含输入函数的差分

能观标准型和能控标准型要知道

第三章

线性时不变系统齐次状态方程的解：$\dot x(t)=Ax(t)$的解为$x(t)=e^{A(t-t_0)}x(t_0)$。

矩阵指数计算记住对角矩阵即可，矩阵指数函数要知道定义式与掌握拉式反变换方法

线性定常系统非齐次状态方程的解，PPT23页的推导： $x(t)=e^{At}x(0)+\int_{0}^{t} e^{A(t-\tau)}Bu(\tau) \, d\tau, t\geq0$

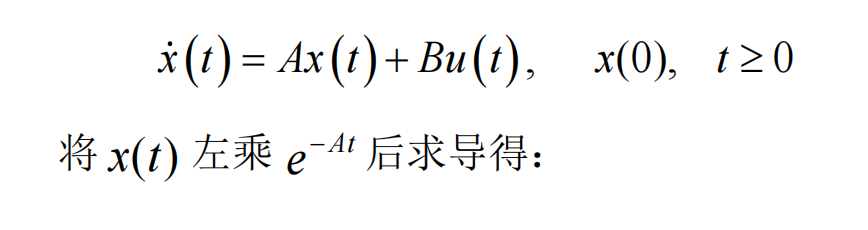
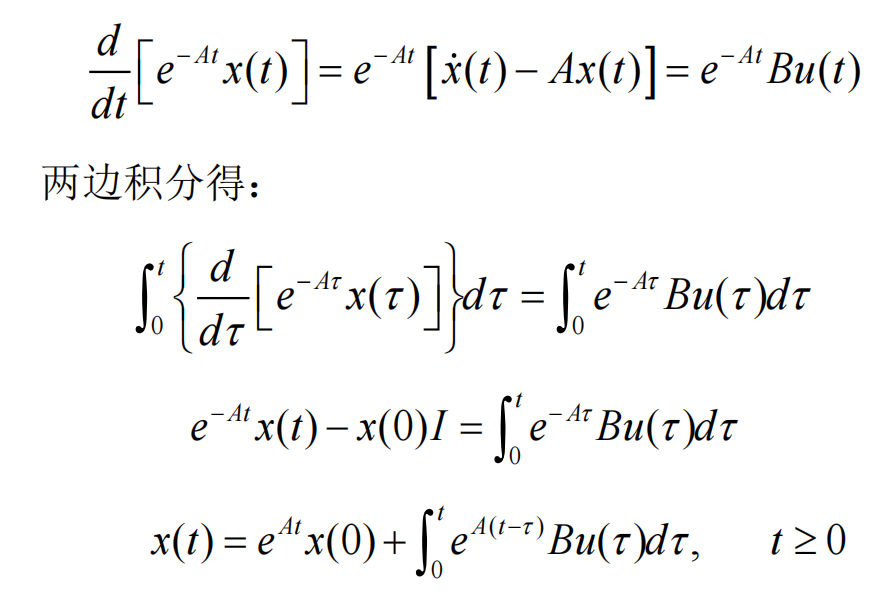
线性时不变系统的状态转移矩阵 $e^{A(t-t_0)}=\Phi(t-t_0)$

线性定常系统的离散化

• 导数近似法会套公式

• ，零阶保持法的G和H要会推导，PPT31页，敲黑板

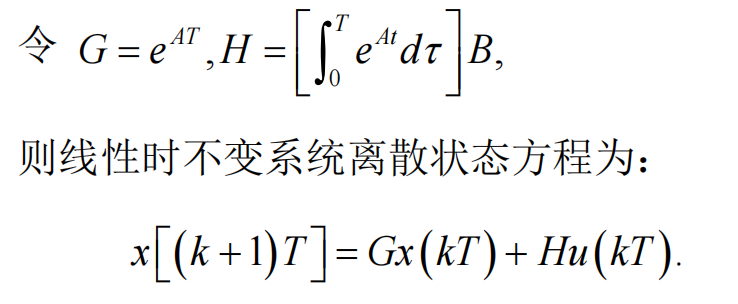
线性离散系统状态方程的解要会递推法

第四章

能控性和能观性的定义、能控性和能观性的判据

• 能控性：
• 能观性：

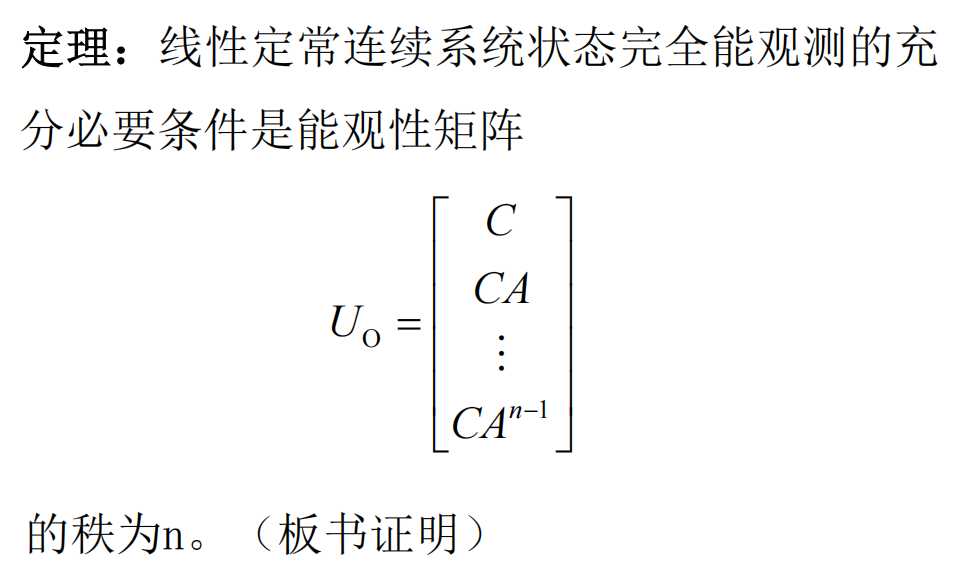
对偶关系

结构分解知道含义就行——采用系统坐标变换的方法对状态空间进行分解，将其划分成能控（能观）部分与不能控（不能观）部分。

能控性、能观性与传递函数矩阵的关系——系统能控能观的充要条件是传递函数g(s)中没有零极点对消现象（单输入单输出系统）

能控标准形和能观标准形知道形式，能化成标准型

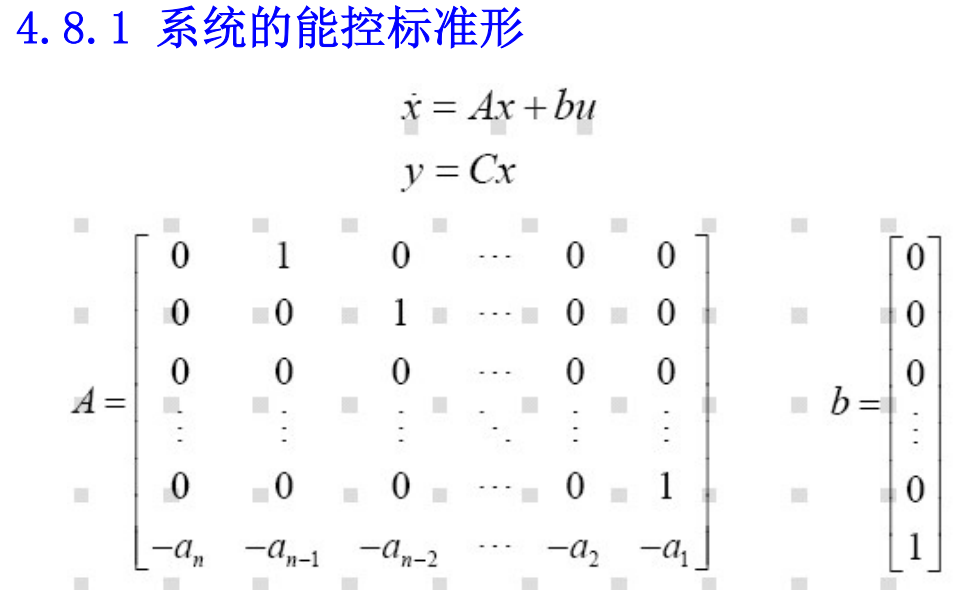
系统的实现——把传递函数化为状态空间模型

最小实现——传递函数矩阵$G(s)$的最小实现$A,B,C$和$D$的充要条件是系统状态完全能控且完全能观测

第五章

平衡状态的含义

李雅普诺夫第一法和第二法

李雅普诺夫意义下的稳定，第7页PPT的图要会结合图来解释稳定、渐进稳定、不稳定

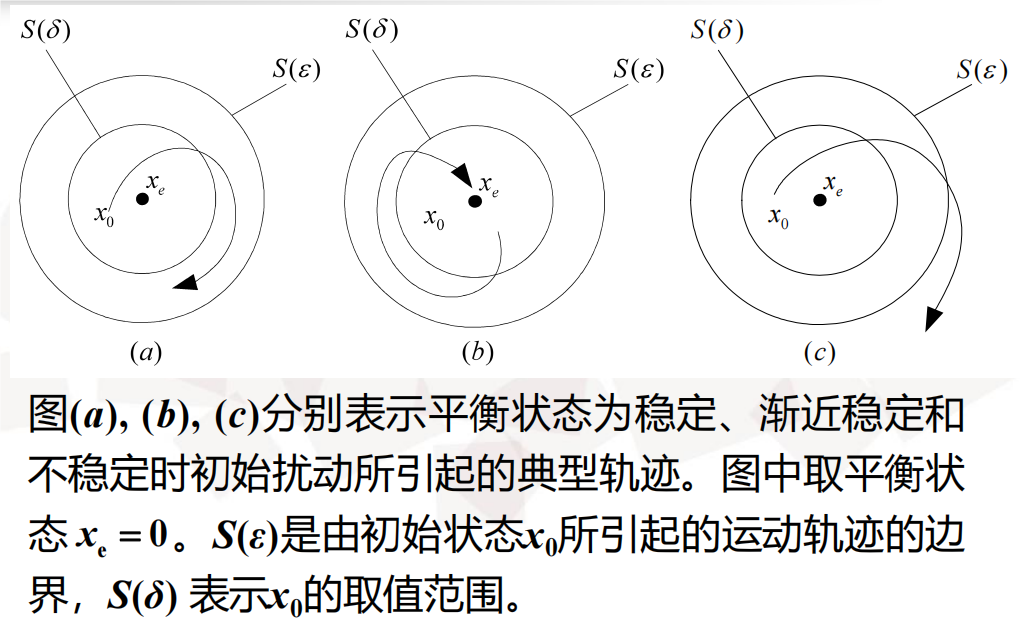
李雅普诺夫稳定性理论（也叫李亚普诺夫稳定性第二方法）的几个定理要会用来判断系统稳定性。

李亚普诺夫方法在线性系统中的应用：PPT24页

第六章

状态反馈的极点配置法

• 极点配置定理

• 解题指导

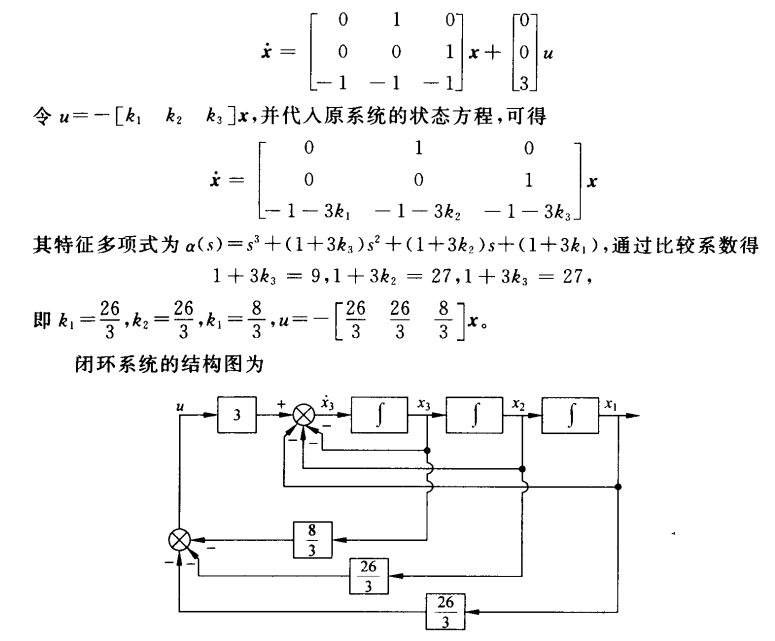
观测器的极点配置

• 线性定常系统的状态观测器存在的充要条件是: 其不能观测的部分是渐进稳定的

• 解题指导

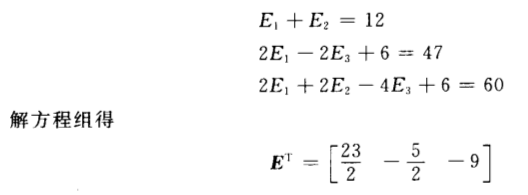
• 降维状态观测器了解概念——当原n维系统的n个状态中有q个可直接量测或通过输出的线性变换可得到, 则只需为剩下的n-q个状态设计n-q维的状态观测器, 这样的状态观测器称为降阶观测器

分离原理要会解释：PPT48页

带有观测器的状态反馈闭环系统的状态空间模型要会写：PPT45页